 Impressum
Impressum

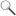 Vergrößern Vergrößern
|
"Jede geschlossene einfach zusammenhängende 3-dimensionale Mannigfaltigkeit ist homöomorph zur 3-Sphäre." Wie O'Shea es gemeistert hat, neben der Geschichte und dem mathematischen Hintergrund, auch den Weg zum Beweis dieser Vermutung so anschaulich und plastisch für Nicht-Mathematiker und Mathematiker zu erzählen, bleibt ein Rätsel.

|
Allgemeines zum Buch
In seinem äußerst lebendig und verständlich geschriebenem Buch zeichnet Donal O’Shea, Professor für Mathematik, die Geschichte der Poincaréschen Vermutung angefangen von ihren Grundlagen bei Pythagoras bis zur Lösung von Grigori Perelman nach. Neben den daraus folgenden Konsequenzen für die Beschaffenheit und den Aufbau unseres Universums, schildert er das Leben und die Arbeiten der größten Mathematiker wie Gauß, Riemann, Klein und Poincaré und gibt auf 377 Seiten einen faszinierenden Einblick in die Gefilde der Topologie.
Das Problem, das hinter der Vermutung von Poincaré steckt, lässt sich folgendermaßen veranschaulichen. Stellen Sie sich vor, Sie machen einen Spaziergang auf der Oberfläche einer Kugel und lassen auf Ihrem Weg einen Faden abrollen. Irgendwann kommen Sie an den Ausgangspunkt Ihres Spazierganges zurück und verknoten die beiden Enden des Fadens. Aufgrund der Struktur der Kugel, können Sie nun ohne Probleme durch Ziehen am Faden, diesen wieder vollständig in Ihre Hand zurückholen. Würden Sie dagegen einen Spaziergang auf einem Torus (ähnlich einem Donut) machen und den Faden nach dem gleichen Prinzip auslegen und verknoten, kann es Ihnen passieren, dass Sie Ihren Faden nicht mehr zurückholen können. In der nebenstehenden Abbildung sind zwei solcher Fäden abgebildet. Generell hat die Oberfläche einer Kugel als einzige “endliche” Fläche (ohne Rand) die Eigenschaft, dass der veknotete Faden nach jedem Spaziergang wieder vollständig aufgerollt werden kann. Man konnte auch relativ einfach gezeigen, dass nur die Oberfläche einer n-dimensionalen Kugel (mit n größer vier) diese Eigenschaft besitzt. Die Poincaré’sche Vermutung verallgemeinert nun diese Behauptung auf die 4-dimensionalen Kugel bzw. auf deren 3-dimensionale Oberfläche, die auch als eine mögliche Struktur unseres Universums in Frage kommen könnte.
Donal B. O’Shea schrieb dieses Buch nicht nur für Mathematiker sondern allgemein für Neugierige, die sich noch an ein bisschen Oberschul-Geometrie erinnern, aber an nicht viel mehr, obwohl auch die mit einem substaziellen mathematischen Hintergrund das Buch gern lesen werden.
Zum Inhalt des Buches
Wagen wir einen kleinen Blick in die einzelnen Kapitel.
Cambridge, April 2003. Jung und alt drängten sich im Hörsaal des MIT (Cambridge). Der Redner, der russische Mathematiker Grigori Perelman, hatte wenige Monate zuvor auf einer Website aufsehnerregende Arbeiten zur Poincaré’schen Vermutung veröffentlicht. Nicht nur Mathematiker, die ebenfalls an der Vermutung arbeiten, sind anwesend, auch die Presse ist auf das sonderbare Genie aufmerksam geworden. Hatten sie doch gehört, dass er an der einen Million Dollar, die auf den Beweis der Vermutung ausgesetzt sind, nicht interessiert sei.
Die Gestalt der Erde. Die Vermutung bietet unter anderen die begrifflichen und mathematischen Mittel, um über die mögliche Gestalt des Universums oder speziell unserer Erde nachzudenken. Die Geschichte, wie die Erde erstmals als kugelförmig verstanden wurde, beginnt 2000 Jahre vor Kolumbus’ Reise. Pythagoras hatte gelehrt, dass die Erde eine Kugel sei. Er hatte Beweise dafür zu sammeln begonnen, und er war der Erste gewesen, der sich vorgestellt hatte, dass die Erde mit den Sternen ein einziges Universum teile. Ausführlich erzählt O’Shea die politischen und sozialen Bezüge der Mathematiker, die an der Erschließung unseres Erdbildes wetteiferten, bis sie so verstanden wurde, wie wir sie heute verstehen.
Mögliche Welten. Am Ende des letzten Kapitels wurde diskutiert, ob die Welt auch ein Torus hätte sein können. Dieses Kapitel bereitet den Leser auf das nächste Kapitel vor, wo es um mögliche Gestalten unseres Universums gehen wird. Es führt dabei so intuitive Begriffe wie Atlanten und deren Karten ein, die für Mathematiker in der Topologie exakte Definitionen besitzen. Aber auch Begrifflichkeiten wie Homöomorphismus und Mannigfaltigen mit oder ohne Rand werden dem Nichtmathematiker spielend einfach vorgestellt.
Die Gestalt unseres Universums. So wie wir die Gestalt der Erdoberfläche mit samt ihrer Krümmung erst vollständig durch Satelliten erschlossen haben, können wir die die Gestalt des 3-dimensionalen Raumes unseres Universums erst erfassen, wenn wir ihn mindestens in 4 Dimensionen sehen können.
Es ist unwahrscheinlich, dass das Universum sich immer und ewig fortsetzt. Das Universum könnte auch einen Rand haben, aber das ist ein bisschen so, also ob man glauben würde, die Erde wäre eine Scheibe. Es gibt nun eine unendliche Menge an möglichen grundsätzlichen Formen für das Universum – Grund genug, hier mit einigen möglichen Kandidaten wie die 3-Sphäre oder einen 4-dimensionalen Donut Bekanntschaft zu machen.
Euklids Geometrie. Die Ergebnisse von über 200 Jahren griechischer Geometrie und Zahlentheorie und 1500 Jahren babylonischer Mathematik sind in den 13 Büchern des Euklids gesammelt. Dabei wurden Schritt für Schritt tiefgründige Aussagen aus den Axiomen gefolgert. Das Werk muss sich aber auch neben den Kritiken über den didaktischen Wert, auch die Frage gefallen lassen, wie schlüssig es ist. Viele Mathematiker waren sich der Schwachstellen Euklids bewusst. Einige davon werden hier kurz angerissen und erweitern zugleich unser Verständnis über den Raum.
Nichteuklidische Geometrie. Für Perelmans Beweis der Poincaré’schen Vermutung muss man wissen, was es bedeutet, dass der Raum gekrümmt ist. Dies führt unweigerlich zu nichteuklidischen Geometrien, wo der Raum negativ oder positiv gekrümmt sein kann. Doch bis sich der radikale Wandel des Denkens in anderen Geometrien vollzogen hatte, gingen noch einige Jahrhunderte ins Land.
Berhard Riemanns Probevorlesung. Der junge Riemann beeinflusste die Mathematik entscheidend und änderte auch die Richtung, in der sich Geometrie und Topologie entwickeln sollten. In seiner Probevorlesung während seiner Habilition, die von Gauss betreut wurde, legte er die Grundlagen für eine Geometrie, indem er Raum und Geometrie begrifflich voneinander trennte bzw. indem er diese als Struktur des Raumes darstellte.
Riemanns Vermächtnis. Es dauerte viele Jahre bis alle Konsequenzen von Riemanns Probevorlesung verstanden und verdauert waren. Dabei sind vor allem die Messungen von positiv und negativ gekrümmten Flächen oder Räumen interessant und der Leser ist dazu eingeladen, sie nachzuvollziehen. William Clifford, ein talentierter Geometer, der als Erster Riemanns Vorlesung ins Englische übersetzte, erkannte sofort das Potenzial der Riemann’schen Geometrie für die Beschreibung physikalischer Phänomene. So zum Beispiel, die stetige Krümmung des Raumes durch Materie, wie sie in Einsteins Relativitätstheorie in Vollendung beschrieben ist.
Klein und Poincaré. Ausführlich geht dieses Kapitel zunächst auf die Biographien der Mathematiker Klein und Poincaré ein. Zudem wird deutlich, wie Poincaré die Topologie und die neuen Sichtweisen von Riemann für sich entdeckt hat und schließlich zu seine Vermutung kam, die er nicht beweisen konnte.
Die großen Gelehrten. Poincarés Arbeiten schlugen ein wie eine Bombe und schufen völlig neue Gebiete in der Mathematik, wie zum Beispiel die algebraische Topologie. Aber die Arbeiten legten auch die Grundlagen zur Relativitätstheorie Einsteins, denn dessen Raumzeit läßt sich durch die Riemann’sche Geometrie mathematisch elegant beschreiben.
Noch ein Mathematiker fehlt in der frühen Historie dieser Vermutung: David Hilbert. In seinem legendären Vortrag zum beginnenden 20. Jahrhundert postulierte er die 13 wichtigsten Probleme, die jeden Mathematiker, der auch nur eines dieser Probleme löst, unsterblich werden lässt.
Die Vermutung setzt sich durch. Kurz vor dem zweiten Weltkrieg war die Poincaré’sche Vermutung zu einem der bekanntesten Probleme der Mathematik geworden. Auch nach dem naiven Optimismus zu Beginn des 20. Jahrhunderts, die Vermutung in kurzer Zeit löst zu haben, arbeiteten die Mathematiker aus der ganzen Welt weiter hartnäckig an diesem Problem. Die Folgen des zweiten Weltkrieges für die deutschen Universitäten und die dort betriebene Mathematik waren irreparabel. Jedoch entwickelten sich außerhalb von Europa weitere große Forschungszentren. Herausragend ist dabei Princeton, welche die namhaftesten europäischen Exil-Mathematiker beherbergte.
Höhere Dimensionen. In den 60er Jahren erlebte die Mathematik und insbesondere die Arbeit an der Vermutung einen riesigen Boom. Auch wenn O. Shea den Nicht-Mathematiker in diesem Kapitel überfordert, so ist doch der so genannte Richie-Fluss ein entscheidender Schlüssel für das Lösen der Poincaré’schen Vermutung. Auch Mathemiker werden nicht darum herumkommen, dieses Kapitel zweimal zu lesen.
Eine Lösung im neuen Jahrtausend. Die beiden letzten Kapitel des Buches konzentrieren sich voll und ganz auf die Person und den Mathematiker Grigori Perelman. Erstaunlich ist, Perelman hat nicht nur die Vermutung Poincarés bewiesen, sondern die so genannte Geometriesierungsvermutung, die die Poincaré’sche Vermutung nur als Spezialfall enthält.
Madrid, August 2006. Nach zweijähriger akribischer Prüfung wurde Perelman bestätigt, den Beweis der Vermutung erbracht zu haben. Im Zuge dessen wurde er für Fields-Medaille nominiert und gewählt. Aber ebenso wie das Preisgeld für den Beweis der Poincaré’schen Vermutung in Höhe von einer Million US-Dollar, war Perelman nicht an der höchsten Ehrung, die einem Mathematiker widerfahren kann, interessiert. So ist das exzentrische Genie auch nicht zur Verleihung der Fields-Medaille erschienen.
Inhaltsverzeichnis